투 포인터 알고리즘(Two Pointers Algorithm) :: DANIDANI

투 포인터 알고리즘은

1차원 배열이 있고 이 배열에서 각자 다른 원소를 가리키고 있는 

2개의 포인터를 조작해가면서 원하는 것을 얻는 형태의 알고리즘이다. 

절대 답이 되지 않는 경우는 계산하지 않아 시간을 단축시켜준다.

 

---

Q. 배열에서 부분 배열의 합이 M이 되는 경우의 수를 구하여라!

 

A1. 가장 쉽고 단순한 방법으로는 이중 for문을 이용해서 모든 경우의 수를 구할 수 있다.

시간 복잡도 O(N^2)

A2. 투 포인터 알고리즘을 이용하면 시간복잡도를 O(N)으로 단축시킬 수 있다.

---

주로 적용되는 문제 유형

- 연속된 수들의 합

- 부분 배열의 합

 

풀이 방법

1. 포인터 2개가 같은 방향으로 진행해 나아가는 것

2. 포인터 2개가 양끝에서 반대로 진행하는 것

 

 

풀이 방법 1,2의 예제를 하나씩 풀어보자

---

 

대표 문제 풀이 1 - 백준 [2003] 수들의 합 2

www.acmicpc.net/problem/2003

 

문제는 간단하다!

배열이 주어지고, 부분 배열의 합이 M이 되는 경우의 수를 구하기!

 

 

문제 접근 방법

1. 2개의 포인터 준비! start, end

start가 가리키는 칸은 포함되고, end가 가리키는 칸은 포함되지 않음.

즉, start == end 인 경우는 크기가 0인 부분 배열을 의미. [start, end)

2. 현재 부분합이 M 이상이면 start ++

3. M 미만이면 end ++

4. 현재 부분합이 M과 같으면 결과 ++

5. 이 과정을 start ≤ end 인 동안 반복!  

---

아래 예제에선 M = 5라고 가정.

start, end는 처음에 모두 인덱스 0을 가리킵니다.

SUM = 2 는 M = 5 보다 작으니 end++

SUM == M 이니 결과를 ++ 해주고 start++

 

end == N 이고, SUM 이 M보다 작거나 같으면 끝이 난다.

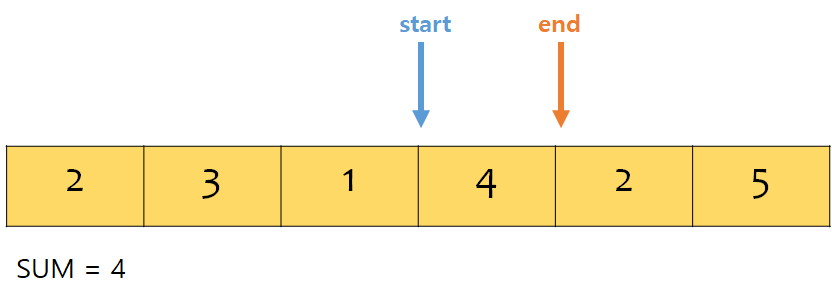
// M : 문제에서 요구하는 합, N : 배열의 길이
int result = 0, sum = 0, start = 0, end = 0;
    while(start <= end){
        if(sum >= M) sum -= arr[start++];
        else if(end == N) break;
        else sum += arr[end++];

        if(sum == M) result++;
    }

 

---

대표 문제 풀이 2 - 백준 [2470] 두 용액

www.acmicpc.net/problem/2470

 

문제는 음수 양수 상관없이 값들을 입력받아서

합이 0에 가장 가까운 두 수를 구하는 것이다.

 

문제 접근 방법

1. 배열을 오름차순으로 정렬

2. 포인터 2개를 준비 Left, Right.

3. Left는 인덱스 0부터 증가, Right는 끝부터 감소.

3. Left + Right > 0 인 경우 합이 더 작아져야 하므로 Right--

4. Left + Right <= 인 경우 합이 더 커 저야 하므로 Left ++

 

sort(arr.begin(), arr.end());

int L = 0, R = N - 1;
while (L < R){
         long long sum = arr[L] + arr[R];
         if (abs(sum) < minimum) {
         	minimum = abs(sum);
            	left = L;
           	right = R;
         }
         if (sum < 0)  L++;
         else R--;
}